PlantUML diagrams without redundancy
PlantUML diagrams without redundancy
tl;dr This blog post demonstrates some practices that use the preprocessor of PlantUML to minimize the amount of redundant code when writing class/sequence diagrams. The presented ideas can be adapted to other PlantUML diagram types to achieve similar benefits.
In order to keep this blog post concise, I’ll walk through a small, condensed example of a software architecture. It is illustrated in form of a class and sequence diagram. All PlantUML diagrams are available on github (download as ZIP).
When rendered, the class and sequence diagrams look like this:
Class diagram _view_class.puml |
Sequence diagram _view_seq.puml |
|---|---|
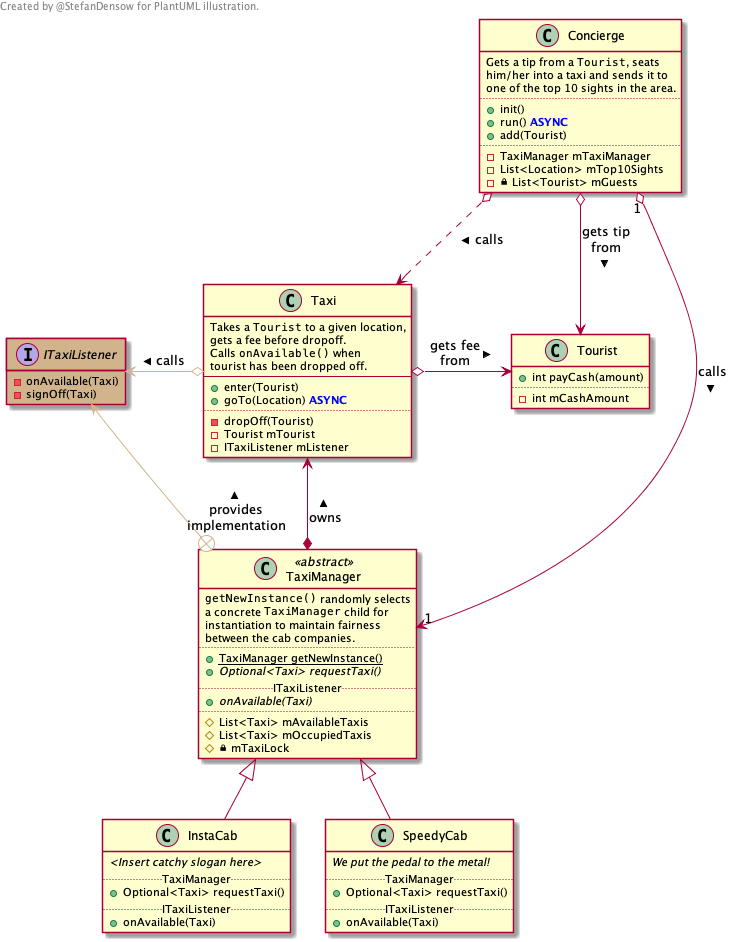 |
 |
The walkthrough assumes some knowledge about PlantUML class and sequence diagram syntax and especially its preprocessing directives.
The example diagrams consist of files which are intended to be rendered (.puml) or included (.iuml):
.puml_view_class.puml- class diagram_view_seq.puml- sequence diagram
.iuml- Preprocessor definitions, variables
_common.iuml- for all diagram types (e.g. color definitions)_common_class.iuml- for class diagrams_common_seq.iuml- for sequence diagrams
- Class diagram content for inclusion in a class diagram
_classes.iuml
- Sequence content description for inclusion in a sequence diagram
Concierge.iumlITaxiListener.iumlSpeedyCab.iumlTaxi.iumlTaxiManager.iumlTourist.iuml
- Preprocessor definitions, variables
Class Diagram: _view_class.puml
The content of each class is written into a separate block in _classes.iuml, each block named exactly the class name. Multiple class diagrams thereby can share the same class content, avoiding redundancy.
Class relations are directly written into _view_class.puml since they generally do not carry over completely to other diagrams, which may show a different subset of classes from _classes.iuml. Also, relations promote a certain layout, as described below.
PlantUML tries to find the optimal class layout using some clever algorithms to let you focus only on the content. These efforts can be supported by following these hints:
- If
Ashould be aboveB,Ashould to be on the left of the arrow, e.g.A --> B. Since the layout engine tries very hard to follow this scheme, I consider this the left-is-up rule (I’m not aware of any other name). - Short arrows as in
A -> Bprefer to generate A left of B whereas longer arrows as inA --> Bprefer to generate A above B. - Additionally, the direction of arrows can be suggested to the layout engine.
Following these hints made my experience with the layout engine much less of a pain.
Sequence Diagram: _view_seq.puml
The class diagram already uses basic preprocessor directives to separate class content from layout and reduce redundancy. With sequence diagrams we’ll turn things up a notch.
Assume a sequence diagram in which a function foo() with a lengthy function body is called several times. The naive way to write the diagram is to duplicate the function content at each call site, i.e. for N calls to foo() the diagram code contains N times the function body. This is horrible for many reasons.
Thanks to the preprocessor, we can do better. We can put the function body into a separate block of a .iuml file and include it where needed. And if foo() calls another function bar(), an !include statement inside the body of foo() does the trick. Include statements are thereby nested exactly the same way as function calls are when the code is executed.
However, apart from the function content we also need some arrows to indicate function entry and return. An additional lifeline activation further improves clarity. All this is packed together inside the CALL_METHOD macro:
!definelong CALL_METHOD(FROM_CLASS, TO_CLASS, FUNC_NAME, ARG = "", RETURN_LABEL = "")
FROM_CLASS -> TO_CLASS: FUNC_NAME(ARG)
activate TO_CLASS
!include_many TO_CLASS.iuml!FUNC_NAME
FROM_CLASS <-- TO_CLASS: RETURN_LABEL
deactivate TO_CLASS
!enddefinelong
It can be used like this: CALL_METHOD(Concierge, TaxiManager, requestTaxi, , empty Taxi) (the fourth argument is left empty to use the fifth).
Hint: Block names can also contain special characters, e.g. id=~CMyClass to denote a C++ destructor.
Note that this macro makes a few assumptions that I personally found reasonable for my purposes.
- Classes are calling methods on each other.
- Methods of a class are stored as separate blocks in a file named
<classname>.iuml.- If a method block is missing, PlantUML ignores that - very useful while writing diagrams.
Actually, there have to be no classes at all - it can also be several sets of functions that belong to some logical purpose. But everything that is supposed to have the same lifeline must be in the same .iuml file.
The example contains an interface (ITaxiListener), which serves as a call target but doesn’t implement any behavior. That, in turn, happens to be implemented by TaxiManager. While this also happens to be the only implementation of ITaxiListener, there could be many implementations in general. However, the sequence diagram should usually show only the behavior of one implementation (if any at all), and ideally this can be switched easily to a different implementation.
This simple forwarding is exactly the purpose of !define ITaxiListener_DELEGATE TaxiManager in ITaxiListener.iuml. This define is used throught the file to forward any incoming call to the delegate object, which provides the actual implementation - in this case TaxiManager. It is also possible to simply cut off after the delegate by creating an empty file called NULL.iuml and adjusting the delegate to !define ITaxiListener_DELEGATE NULL.
A word of caution: The CALL_METHOD macro includes files recursively using !include_many. I.e. if there is any recursion in the function call graph (= the inclusion graph), the result will be an endless inclusion loop, causing PlantUML to go crazy and/or crash. This happens easily, rendering often during editing helps to notice such errors right after they are created.
Conclusion
I hope you find this blog post helpful. I’d love to hear improvements and suggestions!
Thanks to Julia Evans for inspiring me to write this stuff into a blog.